Increase model stability using Bagging in Python

Data scientists usually search for a model that has the highest accuracy possible. However, they should focus on another term too, which is stability. In this article, I explain what it is and how to increase it using a technique called “bagging”.

Bias-variance tradeoff

In machine learning, the prediction error can be decomposed into 3 parts: the squared bias, the variance and the irreducible error. Bias is a measure of how far the predictions are from the real value, variance measures how stable our model is against retraining on a sample created from the original distribution of our dataset and the irreducible error is a noise term that cannot be eliminated. Studying these terms and trying to reduce them is called bias-variance tradeoff.

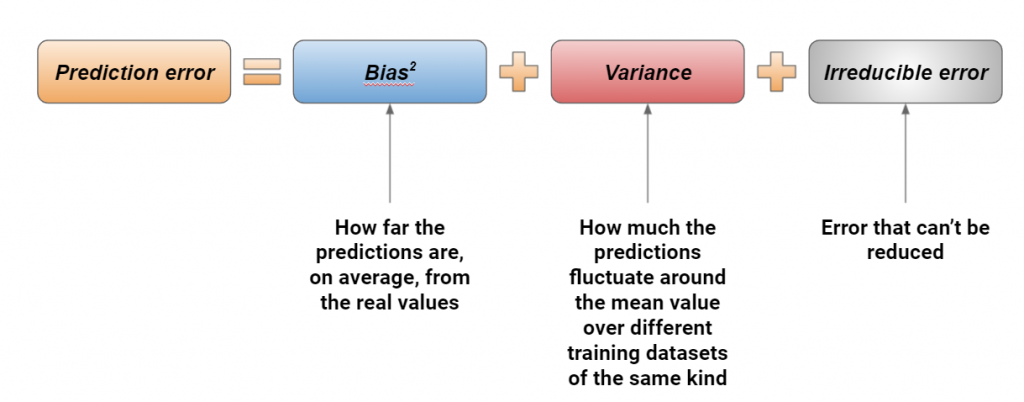
A clearer view of how bias and variance work is given by the following picture. The grey target is the real value, while the red crosses are the predictions made using different resamples of the training dataset.

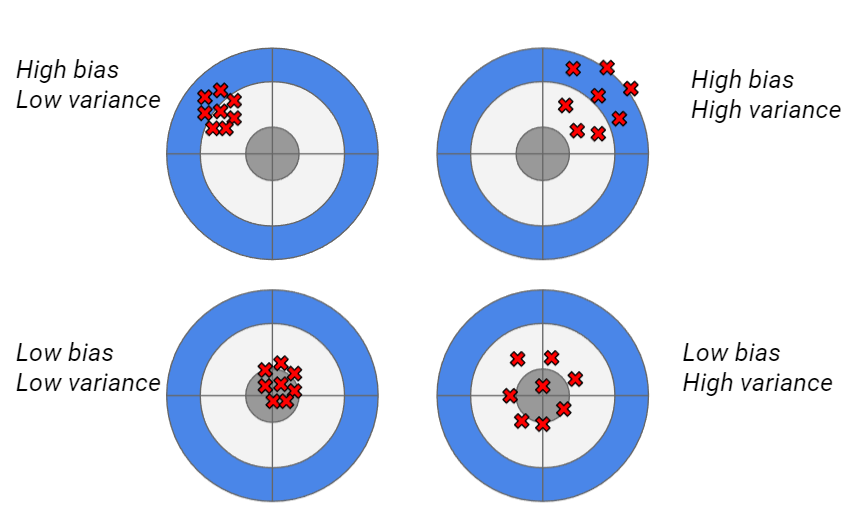
Our goal is to reach the low bias-low variance situation, in which our model is stable against retraining and its predictions are correct. However, models with low bias (like XGBoost) often tend to be unstable over time (high variance) and models with low variance (like a random forest) tend to be less accurate (high bias). A data scientist must know if they want to create an accurate model that is not stable over time (requiring frequent retraining) or a less accurate model that is more stable over time.

Since model training is a very complex and difficult task, I prefer working with models with low variance in order to have a more stable model over time, at the cost of lower performance.

In order to reduce bias, it’s possible to use a technique called boosting. To reduce variance, we can use a technique called bagging. The latter is the topic of this article.

How bagging works

Bagging works following the statistical principle of bootstrapping. Let’s consider all the records and all the features of our dataset.

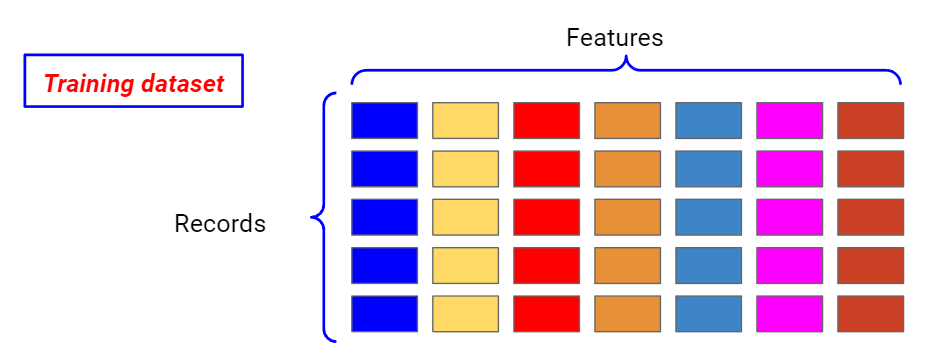
Now, let’s consider some randomly selected samples of our training dataset, sampling our records with replacement and considering a random subset of the columns. This way, we are creating different training datasets we can train our model on, setting the same values of the hyperparameters in advance.

Finally, this ensemble of models can be used to make the final prediction.

For regression problems, the average value of the predictions of the models is often used. For classification, soft voting is the preferred choice.

Bagging mathematically reduces the variance of our model (that is the measure of the fluctuations around the mean performance value when we train our model on different resamples of the original training dataset). The most common bagging model is the random forest, but we can apply the bagging concept to every possible model.

Some bagging techniques bork with a sampling without replacement and the size of the samples can be smaller than the original training dataset size. So, bagging introduces 4 new hyperparameters: the number of samples, the number of columns, the fractions of records to use, whether or not to use sampling with replacement.

Let’s now see how to apply bagging in Python for regression and classification and let’s prove that it actually reduces variance.

Bagging in Python

Let’s now see how to use bagging in Python. The whole code can be found on my GitHub here.

Let’s first import our datasets, which are the breast cancer and diabetes datasets.

from sklearn.datasets import load_breast_cancer,load_diabetes

Let’s now import a regression and a classification model. For regression, we’re going to use linear regression. For classification, we’ll use a Gaussian Naive Bayes model.

from sklearn.linear_model import LinearRegression
from sklearn.naive_bayes import GaussianNB

In order to apply bagging, we have to use a meta-estimator that applies this ensemble technique to a given model. In sklearn we have BaggingRegressor and BeggingClassifier for our purposes. Let’s import them and let’s import cross_val_score in order to calculate the variance.

from sklearn.ensemble import BaggingClassifier,BaggingRegressor


from sklearn.model_selection import cross_val_score

Let’s start with classification. We can import our dataset, train our model and calculate the variance of some performance metric (let’s say the balanced accuracy) over 10-fold cross-validation.

X,y = load_breast_cancer(return_X_y=True)

nb = GaussianNB()

cross_val_score(nb,X,y,scoring="balanced_accuracy",cv=10).var()

# 0.0011182285777794419

This variance is a measure of the stability of the model.

Let’s now apply bagging using, for example, 10 models and half of the original column count. In real-life projects, you want to optimize these values using a hyperparameter tuning technique like grid search.

model = BaggingClassifier(GaussianNB(),n_estimators = 10, max_features = 0.5,random_state = 0, n_jobs = -1)

Variance is, then:

cross_val_score(model,X,y,scoring="balanced_accuracy",cv=10).var()

# 0.000944202642795715

As we can see, it is lower than the original variance. So, bagging has reduced the variance making our model more stable.

We can apply the same concept to regression as well. Let’s use a linear regression model and the R-squared metric.

X,y = load_diabetes(return_X_y=True)

lr = LinearRegression()

cross_val_score(lr,X,y,scoring="r2",cv=10).var()

# 0.021605440351612316

Let’s now apply a BaggingRegressor to our model and calculate the new variance:

model = BaggingRegressor(LinearRegression(),n_estimators = 10, max_features = 0.5,random_state = 0, n_jobs = -1)

cross_val_score(model,X,y,scoring="r2",cv=10).var()

# 0.013136832268767986

It’s half the original value. So, we have created a more stable model.

Conclusions

Bagging is a very useful technique that mathematically increases the stability of a model. I think that it should be preferred to boosting when you know that you won’t be able to train your model again in the future and want to build a model that is stable over time. Of course, monitoring model performance is crucial for the success of a machine learning project, but proper use of boosting makes your model more stable and robust over time, at the cost of lower performance. Sometimes, increasing the stability of a model can be preferred against increasing its accuracy and bagging works exactly this way.